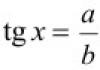Помощь по Теле2, тарифы, вопросы

Что такое обратная функция? Как найти функцию, обратную данной?

Определение .

Пусть функция y=f(x) определена на множестве D, а E — множество её значений. Обратная функция по отношению к функции y=f(x) — это функция x=g(y), которая определена на множестве E и каждому y∈E ставит в соответствие такое значение x∈D, что f(x)=y.

Таким образом, область определения функции y=f(x) является областью значений обратной к ней функции, а область значений y=f(x) — областью определения обратной функции.

Чтобы найти функцию, обратную данной функции y=f(x), надо :

1) В формулу функции вместо y подставить x, вместо x — y:

2) Из полученного равенства выразить y через x:

Найти функцию, обратную функции y=2x-6.

Функции y=2x-6 и y=0,5x+3 являются взаимно обратными.

Графики прямой и обратной функций симметричны относительно прямой y=x (биссектрисы I и III координатных четвертей).

y=2x-6 и y=0,5x+3 — . Графиком линейной функции является . Для построения прямой берём две точки.

Однозначно выразить y через x можно в том случае, когда уравнение x=f(y) имеет единственное решение. Это можно сделать в том случае, если каждое своё значение функция y=f(x) принимает в единственной точке её области определения (такая функция называется обратимой ).

Теорема (необходимое и достаточное условие обратимости функции)

Если функция y=f(x) определена и непрерывна на числовом промежутке, то для обратимости функции необходимо и достаточно, чтобы f(x) была строго монотонна.

Причем, если y=f(x) возрастает на промежутке, то и обратная к ней функция также возрастает на этом промежутке; если y=f(x) убывает, то и обратная функция убывает.

Если условие обратимости не выполнено на всей области определения, можно выделить промежуток, где функция только возрастает либо только убывает, и на этом промежутке найти функцию, обратную данной.

Классический пример — . На промежутке

Е(у) = [-π/2;π/2]

у (-х) = arcsin(-х) = - arcsin х – функция нечетная, график симметричен относительно точки О(0;0).

arcsin х = 0 при х = 0.

arcsin х > 0 при х є (0;1]

arcsin х < 0 при х є [-1;0)

у = arcsin х возрастает при любом х є [-1;1]

1 ≤ х 1 < х 2 ≤ 1 <=> arcsin х 1 < arcsin х 2 – функция возрастающая.

Арккосинус

Функция косинус убывает на отрезке и принимает все значения от -1 до 1. Поэтому для любого числа а, такого, что |а|1, на отрезке существует единственный корень в уравнении cosx=a. Это число в называют арккосинусом числа а и обозначают arcos а.

Определение . Арккосинусом числа а, где -1 а 1, называется такое число из отрезка , косинус которого равен а.

Свойства.

1. Е(у) =

   у(-х) = arccos(-х) = π - arccos х – функция не является ни четной, ни нечетной.

   arccos х = 0 при х = 1

   arccos х > 0 при х є [-1;1)

arccos х < 0 – нет решений

у = arccos х убывает при любом х є [-1;1]

1 ≤ х 1 < х 2 ≤ 1 <=> arcsin х 1 ≥ arcsin х 2 – убывающая.

Арктангенс

Функция тангенс возрастает на отрезке -
, следовательно, по теореме о корне уравнение tgx=a, где а - любое действительное число, имеет единственный корень х на интервале -. Этот корень называют арктангенсом числа а и обозначают arctga.

Определение. Арктангенсом числа a R называется такое число х , тангенс которого равен а.

Свойства.

Е(у) = (-π/2;π/2)

у(-х) = у = arctg(-х) = - arctg х – функция является нечетной, график симметричен относительно точки О(0;0).

arctg х = 0 при х = 0

Функция возрастает при любом х є R

-∞ < х 1 < х 2 < +∞ <=> arctg х 1 < arctg х 2

Арккотангенс

Функция котангенс на интервале (0;) убывает и принимает все значения из R. Поэтому для любого числа а в интервале (0;) существует единственный корень уравнения ctg х = а. Это число а называют арккотангенсом числа а и обозначают arcctg а.

Определение. Арккотангенсом числа а, где а R, называется такое число из интервала (0;), котангенс которого равен а.

Свойства.

Е(у) = (0;π)

у(-х) = arcctg(-х) = π - arcctg х – функция не является ни четной, ни нечетной.

arcctg х = 0 – не существует.

Функция у = arcctg х убывает при любом х є R

-∞ < х 1 < х 2 < + ∞ <=> arcctg х 1 > arcctg х 2

Функция непрерывна при любом х є R.

2.3 Тождественные преобразования выражений, содержащих обратные тригонометрические функции

Пример 1 . Упростить выражение:

а) где

Решение. Положим
. Тогда
и
Чтобы найти
, воспользуемся соотношением
Получаем
Но . На этом отрезке косинус принимает только положительные значения. Таким образом,
, то есть где
.

б)

Решение.

Решение. Положим
. Тогда
и
Найдем сначала , для чего воспользуемся формулой
, откуда
Так как и на этом интервале косинус принимает только положительные значения, то
.

Пусть множества $X$ и $Y$ включены в множество действительных чисел. Введем понятие обратимой функции .

Определение 1

Функция $f:X\to Y$ отображающая множество $X$ в множество $Y$ называется обратимой, если для любых элементов $x_1,x_2\in X$ из того что $x_1\ne x_2$ следует, что $f(x_1)\ne f(x_2)$.

Теперь мы можем ввести понятие обратной функции.

Определение 2

Пусть функция $f:X\to Y$ отображающая множество $X$ в множество $Y$ обратима. Тогда функция $f^{-1}:Y\to X$ отображающая множество $Y$ в множество $X$ определяемая условием $f^{-1}\left(y\right)=x$ называется обратной для $f(x)$.

Сформулируем теорему:

Теорема 1

Пусть функция $y=f(x)$ определена, монотонно возрастает (убывает) и непрерывна в некотором промежутке $X$. Тогда в соответствующем промежутке $Y$ значений этой функции у нее существует обратная функция, которая также монотонно возрастает (убывает) и непрерывна на промежутке $Y$.

Введем теперь, непосредственно, понятие взаимно обратных функций.

Определение 3

В рамках определения 2, функции $f(x)$ и $f^{-1}\left(y\right)$ называются взаимно обратными функциями.

Свойства взаимно обратных функций

Пусть функции $y=f(x)$ и $x=g(y)$ взаимно обратные, тогда

$y=f(g\left(y\right))$ и $x=g(f(x))$

Область определения функции $y=f(x)$ равна области значения функции$\ x=g(y)$. А область определения функции $x=g(y)$ равна области значения функции$\ y=f(x)$.

Графики функций $y=f(x)$ и $x=g(y)$ симметричны относительно прямой $y=x$.

Если одна из функций возрастает (убывает), то и другая функция возрастает (убывает).

Нахождение обратной функции

Решается уравнение $y=f(x)$ относительно переменной $x$.

Из полученных корней находят те, которые принадлежат промежутку $X$.

Найденные $x$ ставят в соответствия числу $y$.

Пример 1

Найти обратную функцию, для функции $y=x^2$ на промежутке $X=[-1,0]$

Так как эта функция убывает и непрерывна на промежутке $X$, то на промежутке $Y=$, которая также убывает и непрерывна на этом промежутке (теорема 1).

Вычислим $x$:

\ \

Выбираем подходящие $x$:

Ответ: обратная функция $y=-\sqrt{x}$.

Задачи на нахождение обратных функций

В этой части рассмотрим обратные функции для некоторых элементарных функций. Задачи будем решать по схеме, данной выше.

Пример 2

Найти обратную функцию для функции $y=x+4$

Найдем $x$ из уравнения $y=x+4$:

Пример 3

Найти обратную функцию для функции $y=x^3$

Решение.

Так как функция возрастает и непрерывна на всей области определения, то, по теореме 1, она имеет на ней обратную непрерывную и возрастающую функцию.

Найдем $x$ из уравнения $y=x^3$:

Находим подходящие значения $x$

Значение в нашем случае подходит (так как область определения -- все числа)

Переопределим переменные, получим, что обратная функция имеет вид

Пример 4

Найти обратную функцию для функции $y=cosx$ на промежутке $$

Решение.

Рассмотрим на множестве $X=\left$ функцию $y=cosx$. Она непрерывна и убывает на множестве $X$ и отображает множество $X=\left$ на множество $Y=[-1,1]$, поэтому по теореме о существовании обратной непрерывной монотонной функции у функции $y=cosx$ в множестве $Y$ существует обратная функция, которая также непрерывна и возрастает в множестве $Y=[-1,1]$ и отображает множество $[-1,1]$ на множество $\left$.

Найдем $x$ из уравнения $y=cosx$:

Находим подходящие значения $x$

Переопределим переменные, получим, что обратная функция имеет вид

Пример 5

Найти обратную функцию для функции $y=tgx$ на промежутке $\left(-\frac{\pi }{2},\frac{\pi }{2}\right)$.

Решение.

Рассмотрим на множестве $X=\left(-\frac{\pi }{2},\frac{\pi }{2}\right)$ функцию $y=tgx$. Она непрерывна и возрастает на множестве $X$ и отображает множество $X=\left(-\frac{\pi }{2},\frac{\pi }{2}\right)$ на множество $Y=R$, поэтому по теореме о существовании обратной непрерывной монотонной функции у функции $y=tgx$ в множестве $Y$ существует обратная функция, которая также непрерывна и возрастает в множестве $Y=R$ и отображает множество $R$ на множество $\left(-\frac{\pi }{2},\frac{\pi }{2}\right)$

Найдем $x$ из уравнения $y=tgx$:

Находим подходящие значения $x$

Переопределим переменные, получим, что обратная функция имеет вид

Функция - это зависимость одной переменной от другой. Функции можно задавать способом таблицы, словесным способом, графический, формулой.

Функции подразделяются на следующие виды:

• Линейная функция
• Квадратичная функция
• Кубическая функция
• Тригонометрическая функция
• Степенная функция
• Показательная функция
• Логарифмическая функция

Область определения функции D(у) - это множество всех допустимых значений аргумента x (независимой переменной x), при которых выражение, стоящее в правой части уравнения функции y = f(x) имеет смысл. Другими словами, это область допустимых значений выражения f(x).

Чтобы по графику функции y = f(x) найти ее область определения, нужно, двигаясь слева направо вдоль оси ОХ, записать все промежутки значений х, на которых существует график функции.

Множество значений фнкции Е(у) - это множество всех значений, которые может принимать зависимая переменная y.

Чтобы по графику функции y = f(x) найти ее множество значений, нужно, двигаясь снизу вверх вдоль оси OY, записать все промежутки значений y, на которых существует график функции.

Обратная функция - функция y=g(x), которая получается из данной функции y = f(x), если из отношения x = f(у) выразить y через x.

Чтобы для данной функции y = f(x) найти обратную, надо:

1. В соотношении y = f(x) заменить x на y, а y - на x: x = f(у) .
2. В полученном выражении x=f(у) выразить y через x.

Функции f(x) и g(x) - взаимно обратны. Рассмотрим это на примере

Примеры нахождения обратных функций:

Область определения и область значений функций f и g меняются местами: область определения f является областью значений g, а область значений f - областью определения g.

Не для всякой функции можно указать обратную. Условие обратимости функции - ее монотонность, то есть функция должна только возрастать или только убывать. Если функция не монотонна на всей области определения, но монотонная на некотором промежутке, тогда можно задать обратную ей функцию только на этом промежутке.

Свойства взаимно обратных функций Отметим некоторые свойства взаимно обратных функций. 1) Тождества .

Пусть f и g – взаимно обратные функции. Тогда: f(g(y)) = у и g(f(x)) = х . 2) Область определения .

Пусть f и g – взаимно обратные функции. Область определения функции f совпадает с областью значений функции g , и наоборот, область значений функции f совпадает с областью определения функции g . 3) Монотонность .

Если одна из взаимно обратных функций возрастает, то и другая возрастает. Аналогичное утверждение верно и для убывающих функций. 4) Графики .

Графики взаимно обратных функций, построенные в одной и той же системе координат, симметричны друг другу относительно прямой у = х .

Преобразования графиков функций - это линейные преобразования функции y = f (x ) или её аргумента x к виду y = af (kx + b ) + m , а также преобразование с использованием модуля.

Зная, как строить графики функции y = f(x) , где

можно построить график функции y = af(kx + b) + m.

Вопросы к конспектам

Y = 0,5x - 4

Найдите область определения функции:

Найдите область определения функции:

Определить четность и нечетность функции:

Решите дробно-рациональное уравнение:

Найдите обратную функцию данной функции:

Найдите значение выражения 6f(-1) +3f(5), если