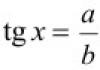Рассмотрим результат наблюдения ^определенной или так называемой детерминированной ФВ Q как случайную величину (СВ), принимающую значения Х } в различных наблюдениях.

Наиболее универсальный способ описания СВ заключается в нахождении их интегральных или дифференциальных функций распределения

Интегральной функцией распределения результатов наблюдений является зависимость от величины х вероятности Р того, что результат наблюдений X. окажется меньше jc. Записывается это следующим образом:

Другими словами, интегральной функцией распределения случайной величины X называется вероятность выполнения неравенства X

Интегральная функция F(x ) обладает следующими свойствами.

• 1. F(x) - неубывающая функция.
• 2. F(x) стремится к единице при jc -> +°°.
• 3. F(x) стремится к нулю при х -> -°о.
• 4. F(х) - функция непрерывная, так как результат наблюдений в определенном интервале может принять любое значение.

Однако четвертое свойство обычно на практике не реализуется. Это обусловлено тем, что применяемые СИ имеют конечное разрешение: для стрелочных приборов - это цена деления шкалы (квант ФВ); для цифровых приборов - это цена наименьшего разряда кода. Поэтому реально функция распределения имеет ступенчатый вид (рис. 4.4).

Несмотря на это, часто в метрологической практике интегральную функцию распределения принимают непрерывной, что значительно упрощает анализ.

Для случайной погрешности, как и для случайной величины, также имеется своя интегральная функция распределения:

Интегральная функция F(x), как и вероятность, является безразмерной величиной.

Более удобно и наглядно описывать свойство результатов наблюдений с помощью дифференциальной функции распределения, которая называется плотностью распределения вероятности. Необходимо отметить, что дифференциальные функции результатов наблюдений X и случайной погрешности А совпадают, только начало координат графика для А располагается в нулевой точке:

График дифференциальной функции распределения или кривая распределения чаще всего представляет собой симметричную функцию с максимумом в точке Q для результатов наблюдений (рис. 4.5). Кривая распределения для случайной погрешности также чаще всего представляет собой симметричную функцию, но с максимумом в точке «О» (рис. 4.6).

Для результатов наблюдений

Для случайной погрешности

Таким образом, дифференциальная функция распределения результатов наблюдений или случайной погрешности получается дифференцированием интегральной функции распределения.

Бывают и несимметричные функции распределения, например функция Релея (рис. 4.7), или функции, не имеющие максимума (равномерная или трапециевидная) (рис. 4.8, 4.9).

Интегральная функция связана с дифференциальной функцией следующим образом:

поскольку , то , т.е. площадь

под кривой функции распределения равна единице. Это и есть так называемое условие нормировки.

Размерность плотности распределения вероятностей обратна размерности измеряемой физической величины, так как интегральная функция распределения является безразмерной. Используя понятие функции распределения, можно получить выражение для вероятности того, что результат наблюдений находится в полуоткрытых интервалах [х, х 2 ] или [А„А 2 ]:

Это выражение говорит о том, что вероятность попадания результата наблюдения X или случайной погрешности измерения А в заданный интервал равна разности значений интегральной функции распределения на указанных границах этого интервала.

Если выразить эту вероятность через дифференциальную функцию распределения или плотность распределения вероятности, то получим:

т.е. вероятность попадания результата наблюдений X или случайной погрешности Д в заданный интервал численно равна площади под кривой плотности распределения вероятности, ограниченной границами интервала (рис. 4.10).

Произведениеp x (x)dx называется элементом вероятности. В том случае, когда закон распределения плотности вероятности близок к так называемому нормальному закону, как видно из графика дифференциальной функции распределения, наиболее вероятны малые значения погрешностей. Вероятность появления больших погрешностей значительно меньше. Результаты наблюдений сконцентрированы вокруг истинного значения измеряемой ФВ, и по мере приближения к нему элементы вероятности возрастают. Это дает основание принять за оценку истинного значения ФВ абсциссу центра тяжести фигуры, образованной осью абсцисс и кривой плотности распределения. Эта характеристика случайной величины называется математическим ожиданием (рис. 4.11):

Теперь можно дать математически строгое определение случайной и систематической погрешности.

Систематическая погрешность 0 (рис. 4.11) - это отклонение математического ожидания результатов наблюдений от истинного значения измеряемой физической величины:

Случайная погрешность А - это разность между результатом единичного наблюдения и математическим ожиданием результатов наблюдений:

Отсюда действительное значение измеряемой физической величины равно

Контрольные вопросы

• 1. Что понимается под дискретной и непрерывной случайными величинами?
• 2. Интегральная функция распределения и ее свойства.
• 3. Дифференциальная функция распределения, связь между интегральной и дифференциальной функциями распределения.
• 4. Условие нормировки интегральной функции распределения.
• 5. Что собой графически представляет математическое ожидание случайной величины?
• 6. Как с физической и математической точек зрения понимать систематическую и случайную составляющие суммарной погрешности?
• 7. Что понимается под элементом вероятности?
• 8. Как определить вероятность попадания результата наблюдений X или случайной погрешности Д в заданный интервал численно, имея график плотности распределения вероятности, ограниченной границами интервала?

В условиях локальной формулы Муавра – Лапласа вероятность того, что число успехов m будет заключено между m 1 и m 2 можно приближенно найти по интегральной формуле Муавра-Лапласа

где x 1 =
, x 2 =
,
-функция Лапласа.

Значения данных функциях есть в приложениях учебников по теории вероятности.

Графическое задание закона распределения представлено на рис. 1

Рис. 1 Полигон распределения дискретной случайной величины.

Способ описания распределения случайной величины в виде таблицы, в виде формулы или графически применим только для дискретных случайных величин.

1.5. Интегральная функция распределения

Интегральная функция распределения позволяет задать как дискретную, так и непрерывную случайную величину.

Интегральная функция распределения (ИФР) – это функция F(x), определяющая для каждого возможного значения x вероятность того, что случайная величина X примет значение меньшее x, т. е.

Геометрический смысл интегральной функции распределения – это вероятность того, что случайная величина X примет значение, которое на числовой оси лежит левее точки x.

Для дискретной случайной величины Х , которая может принимать значения х 1 , х 2 , …,х n , функция распределения имеет вид где неравенство под знаком суммы означает, что суммирование касается всех тех значенийх i , величина которых меньше х . Поясним эту формулу исходя из определения функции F(x ). Предположим, что аргумент х принял какое-то определенное, но такое, что выполняется неравенство x i <x ≤x i +1 . Тогда левее числа х на числовой оси окажутся только те значения случайной величины, которые имеют индекс 1, 2, 3, …, i . Поэтому неравенство Х <x выполняется, если величина Х примет значения х к , где k = 1, 2, …, i . Таким образом, событие Х <x наступит, если наступит любое, неважно какое, из событий Х = х 1 , Х =х 2 , Х =х 3 , …, Х =х i . Так как эти события несовместны, то по теореме сложения вероятностей имеем

Свойства интегральной функции распределения :

1. Значения интегральной функции распределения принадлежат отрезку

:
.

2. Вероятность того, что случайная величина X примет значение, заключенной в интервале (a, b), равна приращению интегральной функции распределения на этом интервале

3. Если все возможные значения x случайной величины принадлежат интервалу (a, b), то

, если

, если

График ИФР непрерывной случайной величины представлен на рис. 2

Рис. 2 График ИФР непрерывной случайной величины

График ИФР дискретной случайной величины представлен на рис. 3

Рис. 3 График ИФР дискретной случайной величины

1.6. Дифференциальная функция распределения

Для описания распределения вероятностей непрерывной случайной величины используется дифференциальная функция распределения.

Дифференциальная функция распределения (ДФР) (или плотность вероятности) – это первая производная от интегральной функции.

Интегральная функция распределения является первообразной для дифференциальной функции распределения. Тогда

Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (a, b), равна определенному интегралу от дифференциальной функции, взятому в пределах от a до b:

Геометрический смысл ДФР состоит в следующем: вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (a, b), равна площади криволинейной трапеции, ограниченной осью x, кривой распределения f(x) и прямыми x = a и x = b (рис. 4).

Рис. 4 График дифференциальной функции распределения принято называть кривой распределения.

Свойства дифференциальной функции распределения:

1. Дифференциальная функция распределения неотрицательна, т. е.

2. Если все возможные значения случайной величины принадлежат интервалу (a, b), то

Дифференциальную функцию распределения часто называют законом распределения вероятностей непрерывных случайных величин.

При решении прикладных задач сталкиваются с различными законами распределения вероятностей непрерывных случайных величин. Часто встречаются законы равномерного и нормального распределения .

Министерство науки и образования РФ

Казанский государственный архитектурно-строительный университет

Кафедра Теплогазоснабжения и вентиляции

по дисциплине «Метрология, стандартизация и сертификация»

Дифференциальные и интегральные функции распределения

Казань 2010 г.

Введение

Глава 2. Числовые параметры законов распределения. Центр распределения. Моменты распределений

Глава 3. Оценка результата измерения

Глава 4. Характеристики нормального распределения

Заключение

Список использованной литературы

Введение

Измерения – один из важнейших путей познания природы человеком. Они играют огромную роль в современном обществе. Наука, техника и промышленность не могут существовать без них. Каждую секунду в мире производятся многие миллиарды измерительных операций, результаты которых используются для обеспечения надлежащего качества и технического уровня выпускаемой продукции, обеспечения безопасной и безаварийной работы транспорта, для медицинских и экологических диагнозов и других важных целей. Практически нет ни одной сферы деятельности человека, где бы интенсивно не использовались результаты измерений, испытаний и контроля.

Поэтому следует говорить об измерительных технологиях, понимаемых как последовательность действий, направленных на получение измерительной информации требуемого качества.

Другой фактор, подтверждающий важность измерений, – их значимость. Основой любой формы управления, анализа, прогнозирования, планирования контроля или регулирования является достоверная исходная информация, которая может быть получена только путем измерения требуемых физических величин, параметров и показателей. Естественно, что только высокая и гарантированная точность результатов измерений обеспечивает правильность принимаемых решений.

Задача, которая ставится перед метрологом, желающим приблизиться к истинному значению измеряемой величины и оценить вероятность определенного отклонения в единичном опыте или в серии измерений, состоит в отыскании закона распределения вероятности получения определенного результата от какого-либо аргумента, связанного с отклонением результата от истинного значения. Наиболее универсальным способом достижения этой цели является отыскание интегральных и дифференциальных функций распределения вероятности.

Глава 1. Вероятностное описание результатов и погрешностей

Если при повторных измерениях одной и той же физической величины, проведенных с одинаковой тщательностью и в одинаковых условиях получаемые результаты, отличаются друг от друга, то это свидетельствует о наличии случайных погрешностей. Случайные погрешности являются результатом одновременного воздействия на измеряемую величину многих случайных возмущений. Предсказать результат наблюдения или исправить его введением поправки невозможно. Можно лишь с определенной долей уверенности утверждать, что истинное значение измеряемой величины находится в пределах разброса результатов наблюдений от x min до x max , где x min , x max – соответственно, нижняя и верхняя границы разброса.

Однако остается неясным, какова вероятность появления того или иного значения погрешности, какое из множества лежащих в этой области значений величины принять за результат измерения и какими показателями охарактеризовать случайную погрешность результата. Для ответа на эти вопросы требуется принципиально иной, чем при анализе систематических погрешностей, подход. Подход этот основывается на рассмотрении результатов наблюдений, результатов измерений и случайных погрешностей как случайных величин. Методы теории вероятностей и математической статистики позволяют установить вероятностные (статистические) закономерности появления случайных погрешностей и на основании этих закономерностей дать количественные оценки результата измерения и его случайной погрешности.

Для характеристики свойств случайной величины в теории вероятностей используют понятие закона распределения вероятностей случайной величины. Различают две формы описания закона распределения: интегральную и дифференциальную. В метрологии преимущественно используется дифференциальная форма – закон распределения плотности вероятностей случайной величины.

Рассмотрим формирование дифференциального закона на примере измерений с многократными наблюдениями. Пусть произведено n последовательных наблюдений одной и той же величины x и получена группа наблюдений x 1 , x 2 , x,..., x n . Каждое из значений x i содержит ту или иную случайную погрешность. Расположим результаты наблюдений в порядке их возрастания, от x min до x max и найдем размах ряда L = x max − x min . Разделив размах ряда на k равных интервалов Δl = L / k, подсчитаем количество наблюдений n k , попадающих в каждый интервал. Оптимальное число интервалов определяют по формуле Стерджесса k = 1÷3,3 lg n. Изобразим полученные результаты графически, нанеся на ось абсцисс значения физической величины и обозначив границы интервалов, а на ось ординат – относительную частоту попаданий n k / n. Построив на диаграмме прямоугольники, основанием которых является ширина интервалов, а высотой n k / n, получим гистограмму, дающую представление о плотности распределения результатов наблюдений в данном опыте.

На рис. 1 показана полученная в одном из опытов гистограмма, построенная на основании результатов 100 наблюдений, сгруппированных в таблице 1.

Таблица 1

В данном опыте в первый и последующие интервалы попадает соответственно 0,06; 0,12; 0,18; 0,25; 0,17; 0,14 и 0,08 от общего количества наблюдений; при этом, очевидно, что сумма этих чисел равна единице.

Рис. 1. Гистограмма

Если распределение случайной величины х статистически устойчиво, то можно ожидать, что при повторных сериях наблюдений той же величины, в тех же условиях, относительные частоты попаданий в каждый интервал будут близки к первоначальным. Это означает, что построив гистограмму один раз, при последующих сериях наблюдений можно с определенной долей уверенности заранее предсказать распределение результатов наблюдений по интервалам. Приняв общую площадь, ограниченную контуром гистограммы и осью абсцисс, за единицу, S 0 =1, относительную частоту попаданий результатов наблюдений в тот или иной интервал можно определить как отношение площади соответствующего прямоугольника шириной Δl к общей площади.

При бесконечном увеличении числа наблюдений n→ ∞ и бесконечном уменьшении ширины интервалов Δl →0, ступенчатая кривая, огибающая гистограмму, перейдет в плавную кривую f (x) (рис. 2), называемую кривой плотности распределения вероятностей случайной величины, а уравнение, описывающее ее, – дифференциальным законом распределения. Кривая плотности распределения вероятностей всегда неотрицательна и подчинена условию нормирования в виде

Рис. 2. Кривая плотности распределения вероятностей

Закон распределения дает полную информацию о свойствах случайной величины и позволяет ответить на поставленные вопросы о результате измерения и его случайной погрешности. Если известен дифференциальный закон распределения f (x), то вероятность Ρ попадания случайной величины х в интервал от x 1 до x 2 можно записать в следующем виде

Графически эта вероятность выражается отношением площади, лежащей под кривой f (x) в интервале от x 1 до x 2 к общей площади, ограниченной кривой распределения. Следовательно, рассмотренное выше условие нормирования означает, что вероятность попадания величины х в интервал [− ∞; + ∞] равна единице, т.е. представляет собой достоверное событие. Вероятность этого события называется функцией распределения случайной величины и обозначается F(x). Функцию распределения F(x) иногда называют также интегральной функцией распределения. В терминах интегральной функции распределения имеем

P {x 1 ≤ x ≤ x 2 }= F (x 1)− F (x 2),

т.е. вероятность попадания результата наблюдений или случайной погрешности в заданный интервал равна разности значений функции распределения на границах этого интервала.

Рис. 3. Интегральная (а) и дифференциальная (б) функции распределения случайной величины

Интегральной функцией распределения F(x) называют функцию, каждое значение которой для каждого х является вероятностью события, заключающегося в том, что случайная величина x i в i -м опыте принимает значение, меньшее х. График интегральной функции распределения показан на рис. 3, а. Она имеет следующие свойства:

− неотрицательная, т.е. F(x) ≥ 0;

− неубывающая, т.е. f (x 2) ≥ F(x 1), если x 2 ≥ x 1 ;

− диапазон ее изменения: от 0 до 1, т.е. F(−∞) = 0; F(+∞) = 1;

− вероятность нахождения случайной величины х в диапазоне от x 1 до

x 2: P{x 1 < x < x 2 }= F(x 2) − F(x 1).

Запишем функцию распределения через плотность:

Площадь, ограниченная кривой распределения, лежащая левее точки x (х

– текущая переменная) (рис. 4), отнесенная к общей площади, есть не что иное, как интегральная функция распределения F(x) = P{x i < x}.

Обозначим через вероятность того, что случайная величина х принимает значение меньше являющаяся функцией называется интегральной функцией распределения величины х. Поскольку любая вероятность должна лежать в интервале между и 1, то для всех значений имеем: Если таковы, что вероятность того, что будет больше или равна вероятности того, что т. е. Другими словами, функция не может уменьшаться с возрастанием

Типичная форма интегральной функции распределения показана на рис. 1, где по горизонтальной оси отложено а по вертикальной функция

Зная интегральную функцию распределения легко можем для любых заданных определить вероятность того, что Действительно, поскольку события несовместны, то вероятность осуществления какого-либо из этих событий будет равна сумме вероятностей осуществления каждого из событий, т. е.

(см. скан)

Поскольку вероятность осуществления какого-либо из этих двух событий или совпадает с вероятностью осуществления события то в соответствии с соотношением (1.1) имеем

Следовательно, искомая вероятность осуществления события будет равна

В случае, когда случайная величина х является результатом измерения какой-либо характеристики объекта, случайным образом выбранного из группы объектов, можно дать простое толкование интегральной функции распределения Как указывалось в п. 1.1.1, в этом случае вероятность того, что наблюденная величина х удовлетворяет некоторому равенству или неравенству (скажем, или равна относительной доле (в данной группе из объектов) таких объектов, для которых величина х удовлетворяет соответствующему равенству или неравенству. Таким образом, просто определяет относительную долю тех объектов, для которых При таком истолковании вероятностей соотношение (1.2) становится очевидным. Оно, собственно, утверждает, что относительное количество объектов, для которых равно относительному количеству объектов, для которых плюс относительное количество объектов, для которых Группа из объектов часто называется генеральной совокупностью. До сих пор мы рассматривали только генеральные совокупности, содержащие конечное число объектов. Такие генеральные совокупности называются конечными.

Истолкование вероятности события, для которого выполняется определенное соотношение (равенство или неравенство), как относительной доли в данной генеральной совокупности таких элементов, для которых величина х удовлетворяет этому соотношению, оказывается во многих случаях весьма полезным, и мы будем им часто пользоваться. Однако такая интерпретация вероятностей не всегда возможна, если мы не ограничиваемся конечными генеральными совокупностями. Действительно, интегральная функция распределения, связанная с конечной генеральной совокупностью, имеет свои особенности.

Предположим, что генеральная совокупность состоит из элементов. Тогда случайная величина х может принимать не более различных значений. Пусть различные значения, которые может принимать величина х, причем эти значения расположены в возрастающем порядке, Ясно, что Если величина х одинакова для нескольких элементов, то Интегральная функция распределения в этом случае будет иметь вид ступенчатой кривой, показанной на рис. 2.

Функция распределения будет иметь ровно скачков, причем величина каждого скачка будет равна либо либо целому числу, умноженному на Интегральная функция распределения, представленная непрерывной кривой рис. 1, очевидно, не относится к этому типу.

Таким образом, если интегральная функция распределения является непрерывной кривой, то истолкование вероятностей как относительной доли определенных элементов конечной генеральной совокупности оказывается невозможным. Однако любую непрерывную интегральную функцию распределения можно с любой заданной точностью аппроксимировать ступенчатой интегральной функцией распределения, связанной с конечной генеральной совокупностью, если только число элементов в последней достаточно велико. Таким образом, любую непрерывную интегральную функцию распределения можно считать предельной формой интегральной функции распределения, связанной с конечной генеральной совокупностью. Предел достигается при бесконечном возрастании числа элементов в этой генеральной

совокупности. Это означает, что если мы допускаем существование бесконечной генеральной совокупности (генеральной совокупности с бесконечно большим числом элементов), то любую вероятность, связанную с этой совокупностью, всегда можно истолковать как относительную долю соответствующих элементов совокупности. Конечно, понятие бесконечной генеральной совокупности является просто полезной абстракцией, вводимой лишь для упрощения теории.

В качестве примера бесконечной генеральной совокупности рассмотрим эксперимент, заключающийся в измерении длины некоторого стержня. Исход каждого измерения можно считать случайной величиной, характеризующейся интегральной функцией распределения Тогда бесконечной генеральной совокупностью будет бесконечная последовательность повторяющихся измерений длины стержня, так что каждое действительно произведенное измерение можно считать элементом этой совокупности. Иногда генеральная совокупность является конечной, но число элементов этой совокупности настолько велико, что оказывается удобнее рассматривать задачи, связанные с этой совокупностью, так, как если бы было бесконечным, т. е. как если бы генеральная совокупность была бесконечной. Предположим, например, что мы интересуемся распределением роста всех женщин в возрасте 20 лет и старше, проживающих в Соединенных Штатах. Очевидно, что количество таких индивидуумов настолько велико, что можно рассчитывать на значительные математические упрощения, если считать генеральную совокупность таких индивидуумов бесконечной.